Rätseln mit Eder: Wie viele Enkel haben die Großeltern höchstens?
Für ihre Enkelkinder haben sich die Großeltern eine kleine Überraschung ausgedacht: Jedes Kind erhält einen Beutel mit Münzen. Insgesamt haben sie 48 Münzen im Wert von 72 Euro besorgt, 24 Zwei-Euro-Münzen und 24 Ein-Euro-Münzen. Sie haben sämtliche 48 Münzen verteilt.
In jedem Beutel befindet sich die gleiche Anzahl Zwei-Euro-Münzen, doch in keinem Beutel sind gleich viele Ein-Euro-Münzen. Das Besondere: Jeder Betrag stimmt jeweils genau mit dem Alter des beschenkten Kinds überein.
Wie viele Enkelkinder können die Großeltern höchstens haben?
Zusatzfrage: Warum lässt sich das Alter der Kinder nicht eindeutig bestimmen?
Die Großeltern haben sechs Enkelkinder.
Erklärung
Um diese Aufgabe zu meistern, helfen die folgenden Überlegungen:
1. Da sich in jedem Beutel die gleiche Anzahl Zwei-Euro-Münzen befinden, muss die Anzahl der Beutel ein Teiler von 24 sein. Die Zahlen 1, 2, 3, 4, 6, 8, 12 und 24 erfüllen diese Bedingung. Damit sind zunächst alle Möglichkeiten für die gesuchte Anzahl von Enkelkindern gefunden, die als Lösung infrage kommen.
2. Da sich in keinem Beutel gleich viele Ein-Euro Münzen befinden und gleichzeitig gefragt war, wie viele Enkelkinder es höchstens sein können, ist es ratsam, möglichst wenige Münzen auf die einzelnen Beutel zu verteilen, um eine möglichst große Anzahl von Geldbeuteln zu erreichen:
Laden...21 Münzen lassen sind auf genau sechs Beutel verteilen. Die drei restlichen Münzen können zu den 4, 5 oder 6 Münzen dazugegeben werden, denn sie reichen nicht für einen siebten Geldbeutel. Zusammen mit den vier Zwei-Euro-Münzen in jedem Geldbeutel ergibt sich die folgende mögliche Geldverteilung:
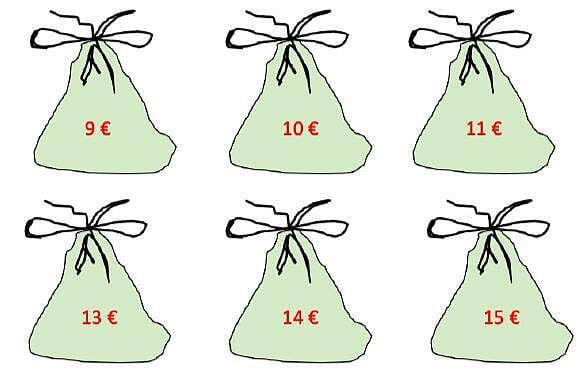Laden...Antwort auf die Zusatzfrage: Da man die Verteilung nicht eindeutig vornehmen kann, lässt sich leider nicht eindeutig bestimmen, wie alt jedes Kind ist.
Aufgabe und Lösung im Video
Rätseln mit Eder: Wie viele Enkel haben die Großeltern höchstens? - Spektrum der Wissenschaft
Read More
No comments:
Post a Comment